虚数 （17世纪著名数学家笛卡尔创立的数学用语）

简介

17世纪著名数学家、哲学家笛卡尔（Descartes，R.）所著《几何学》（法语：La Géométrie）一书中，命名其为nombre imaginaire（虚构的数），成为了虚数（imaginary number）一词的由来。

早期数学家试图通过引入“虚数”来解决数学中的无解问题，虚数的起源可以追溯到16世纪，意大利数学家吉罗拉莫·卡尔达诺（Cardano,G）提出虚数的概念，他认为虚数是一个虚构的数，其平方根为复数。

1777年瑞士科学家欧拉（Euler，L.）系统地建立了复数理论，同时引进了虚数单位的符号“i”。虽然复数的概念最初是为了解决数学中的无解问题而引入的，但随着时间的推移，人们发现复数在许多实际应用中具有重要意义。例如，在数学知识应用中，复数的使用简化了复杂的数学计算；在量子力学中，波函数通常表示为复数形式；在物理中，复数可以用于表示物体的运动规律，运用复数性质进行轨迹的分析及描述。

虚数定义

在数学里，将偶指数幂是负数的数定义为纯虚数。所有的虚数都是复数，定义为

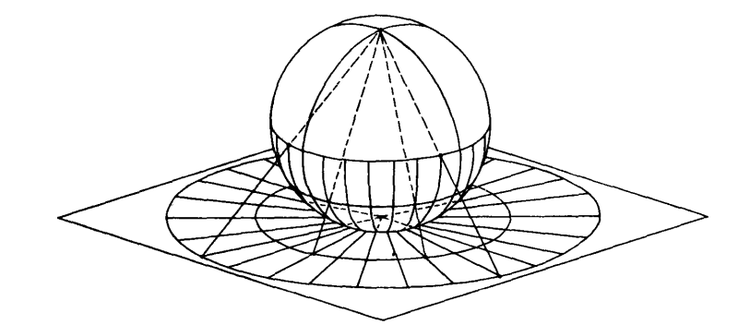
把复数几何地表示为平面上的点的思想是高斯于1799年在他的学位论文中简明陈述的，阿尔冈(Argand)于 1806 年也独立地提出，后来高斯创造了“复数”这个多少有点儿令人遗憾的词汇，也可以用别的方式对复数进行几何解释，如果不用平面上的点，也可以使用某种曲面上的点，黎曼(Riemann)就发现使用球面特别方便:从北极把球面上的点投影到南极处的切平面上，则这个切平面上的每一个点有球面上确定的点与之对应，除了北极点本身以外，球面上的每个点都恰好对应于这个切平面上的一个点。这种对应称为球极平面投影(见图 3-1)。

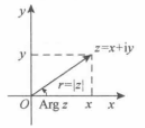
向量表示法

由向量的点表示法可得，复数

三角表示法

对于复数的代数性质

因此，

显然复数

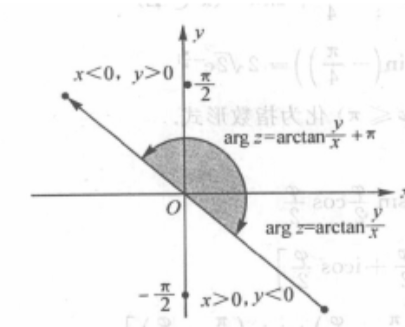
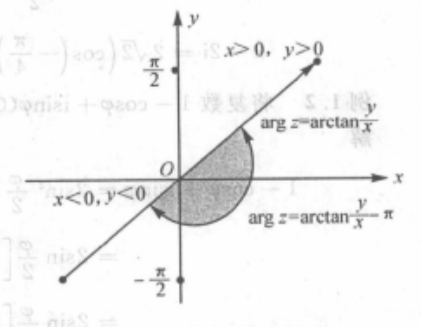
由该公式可以推出：

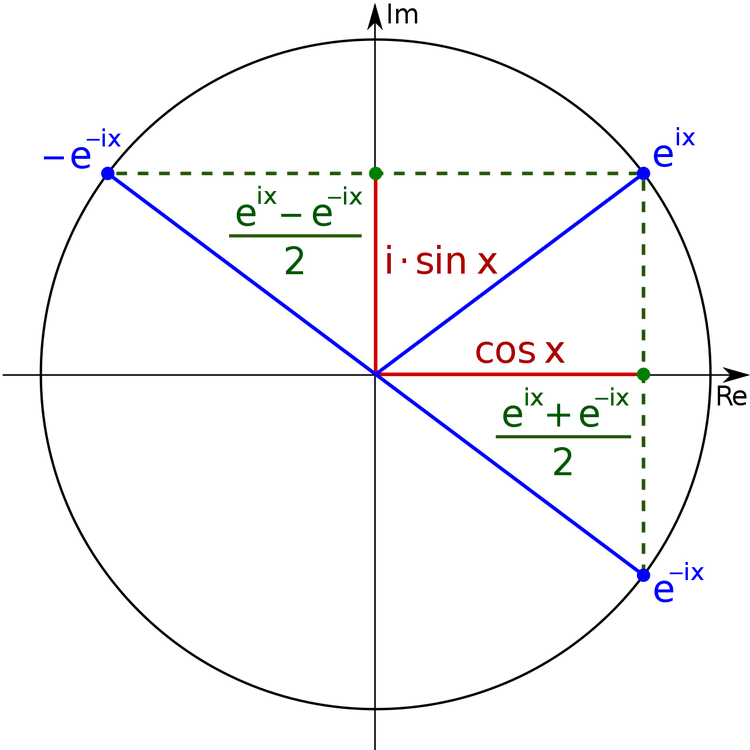
同时，欧拉公式充分显示了虚数的旋转特征，指数函数

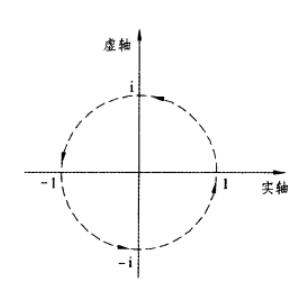
基本运算

复数的加法

复数加法指复数和的运算，两个复数相加，实部是原来两个复数实部的和，虚部是原来两个虚部的和，即：

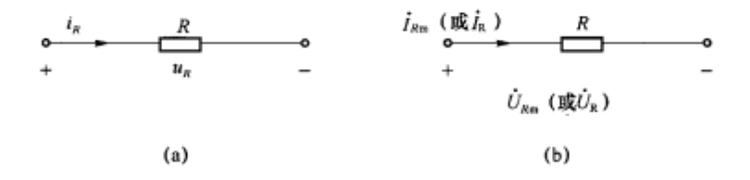
电容组件的复数模型

如图 7.2(a)中电容电流

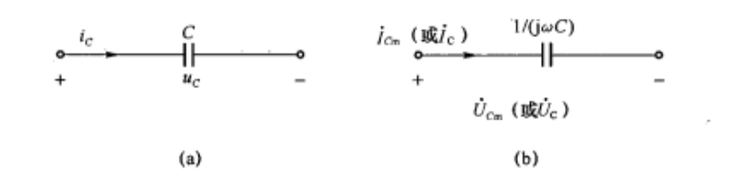
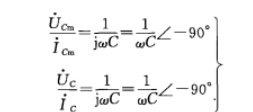
若

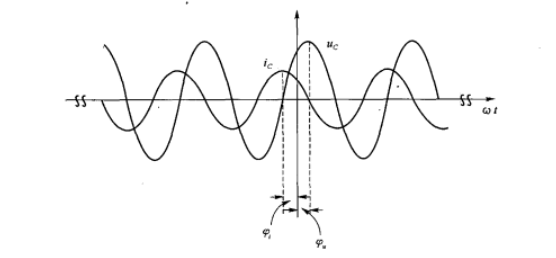
式（7-2）称为电容元件的复数欧姆定律它表明了正弦电路中电容元件的电压相量与电流相量的正比关系。比例系数

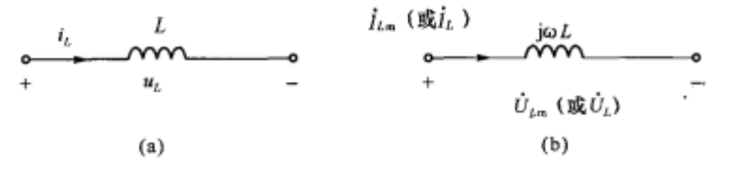
在正弦情况下,若

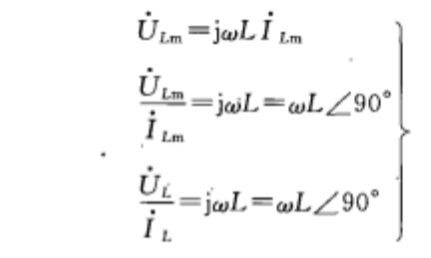
由此可得出电感元件的复数模型为

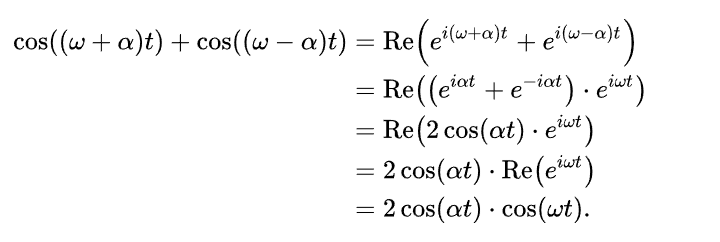
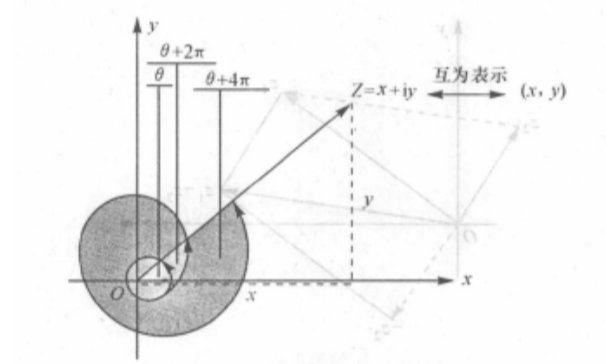
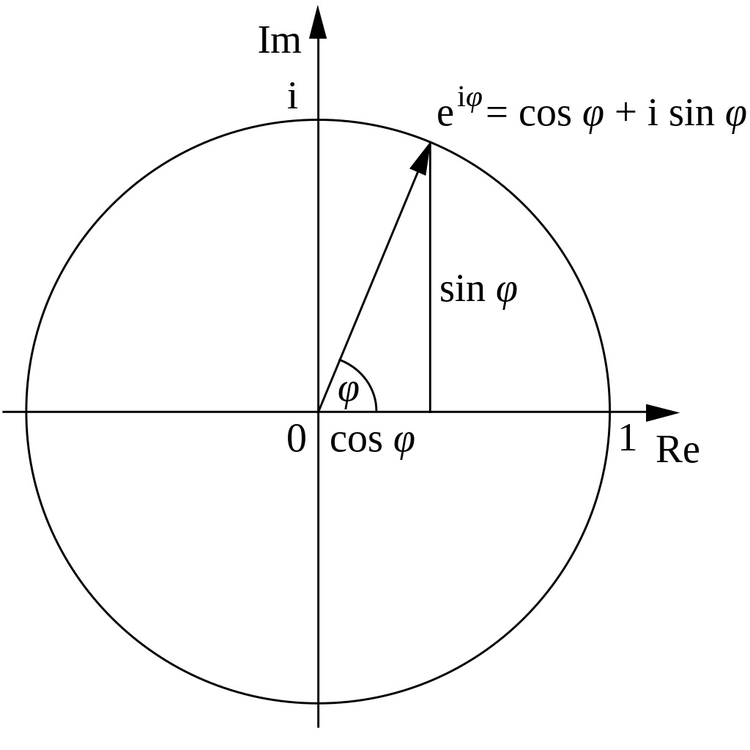
欧拉公式

欧拉公式指出，对于任何实数y，

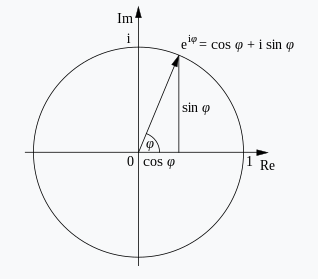
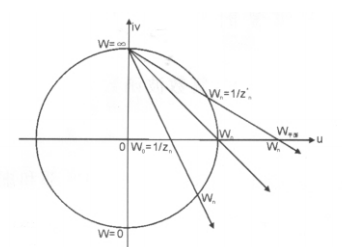
图中复平面：

注释

如果x是复数，该公式仍然有效