定义
光与实物粒子具有粒子性也具有波动性,粒子性是指粒子有质量、动量和能量、占据一个很小的空间任意时刻位置由运动方程确定、有确定的运动轨道等特性,光的粒子性在于其具有粒子的某些特性又不完全与粒子相同,光没有确定的位置、没有确定的运动轨道;波动性是指波具有的能够时变电磁场在空间传播、有叠加性、衍射性和可分性、能展布在一个较大的空间等特性,实物粒子的波动性在于其具有波的某些特性。电子等实物粒子具有波粒二象性,具体是指,对于一个质量为
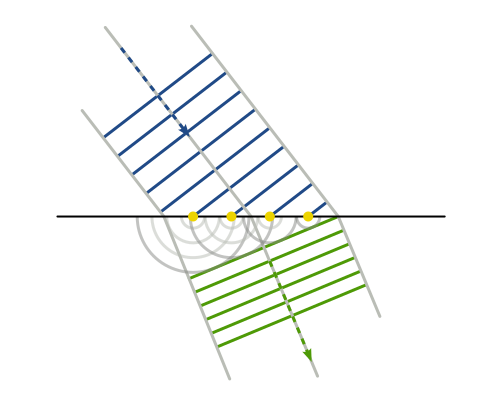
惠更斯-菲涅尔原理
菲涅尔(Fresnel)发展了惠更斯原理,提出惠更斯-菲涅尔原理,认为波阵面上的每一点都可看作一个子波源,这些子波源是相干波源,它们发出的光波在空间相遇以后发生相干迭加,迭加产生的光强分布产生了衍射图样。惠更斯-菲涅尔原理的假设计算:
设有波阵面S,从S上取出一小块面积ds,ds即为一个子波源,该子波源在P点产生的光振动为

麦克斯韦、赫兹与电磁波
麦克斯韦(Maxwell)在总结前人的理论和实验的基础上,把电磁理论概括为麦克斯韦方程,预言了电磁波的存在,计算出电磁波在媒质中的传播速度与光在同一媒质中的传播速度相等,由此认为光也是一种电磁波。后来,赫兹(Hertz)通过实验证实了电磁波的存在,研究证明了电磁波具有与光波相同反射、折射、干涉、衍射和偏振的性质,并测出电磁波的传播速度等于光速。麦克斯韦方程从理论和实验上证明了光是电磁横波,确立了光的电磁波理论,进一步验证了光的波动说。
普朗克黑体辐射定律
黑体是一个自然界和工程应用中不存在的完全理想化的概念,是指一种能够吸收来自所有频率、所有入射方向的电磁波而没有反射的理想物体。普朗克黑体辐射定律描述了在任意温度下从一个黑体发射的电磁辐射的辐射率与其频率的关系,公式:
1927年戴维孙(Davisson)和革末(Germer L H)用加速后的电子投射到晶体上进行电子衍射实验,证实了电子的波动性。同年,G.P汤姆逊(Thomson G P)做了电子衍射实验,将电子束穿过金属片(多晶膜),在感光片上产生圆环衍射图和X光通过多晶膜产生的衍射图样极其相似,同样证实了电子的波动性。
海森堡不确定性原理
海森堡(Heisenberg)的不确定性原理认为,由于微观粒子具有波动性,以致它的某些成对物理量(如粒子的位置和速度)无法同时精确地测量,测量一个物理量就会不可避免地对另一个物理量产生扰动,测量得越准确扰动越强,同时测量的精确度存在一个极限,粒子位置的不确定性

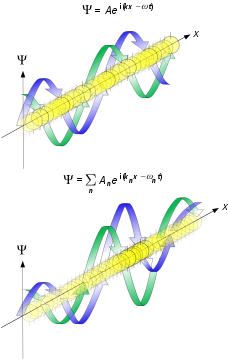
薛定谔方程
波函数满足微观领域的基本方程——薛定谔方程,三维空间中的一般定态薛定谔(Erwin Schrödinger)方程为:


双孔干涉实验
1800年,托马斯·杨发表了题为《在声和光方面的实验和问题》(《Experiments on Sound and Light 》)的论文,认为声和光都是波的传播,光是发光以太中类似于声波的纵振动;光的颜色和不同频率的声音是一样的。1801年,托马斯·杨提出干涉定律并通过著名的双孔干涉实验演示了光的干涉现象。

量子论的“奠定”——普朗克黑体辐射定律
1900年,普朗克在量子理论的基础上提出了普朗克黑体辐射定律(又称普朗克定律或黑体辐射定律),提出一种能够吸收来自所有频率、所有入射方向的电磁波而没有反射的理想物体"——“黑体”,并给出了在任意温度下从一个黑体发射的电磁辐射的辐射率与其频率的关系式,奠定了量子理论的基础。
波粒二象性的提出
1905年,爱因斯坦在德国《物理年报》(《Annals of Physics 》)上发表了题为《关于光的产生和转化的一个推测性观点》的论文,解释光电效应(光照射在碱金属上引起电子发射的现象),并给出了光电效应方程,认为光具有波粒二象性,既具有干涉、衍射等波的性质,又具有被吸收、发射、有动量等粒子的性质,这一观点得到广泛认可。1921年,爱因斯坦因为“光的波粒二象性”这一成就而获得了诺贝尔物理学奖。

波粒二象性的拓展
1924年,德布罗意在博士学位论文中将波粒二象性推广到所有的实物粒子,认为实物粒子也具有波动性,任何物体伴随着波,不可能将物体的运动和波的传播分开,物体的波称为德布罗意波。

波粒二象性的验证
1926年,波恩提出“统计解释”,指出了德布罗意波的统计意义,认为物质波在本质上是一种概率波,粒子在各处出现的概率随物质波强度的分布。1927年,德布罗意的假设分别被戴维孙与革末的电子束在镍单品上反射实验及G.P.汤姆逊做的电子衍射实验从电子层面印证了德布罗意波。


1927年,海森堡提出“不确定性原理”(也称“测不准原理”),认为对于电子这样小尺度的事物,在测量时不可避免地会产生不容忽视的影响,使得其共轭变量难以同时测出;同年,玻尔提出了“互补性原理”,认为物体的波动性与粒子性互补,在粒子和波的双重基础之上才能准确描述物质。1929年,斯特曼(Stormare)、斯特恩(Stern)用氮原子和氢分子束通过氟化锂晶体进行衍射实验,验证了原子和分子的波动性;同年,德布罗意因为“德布罗意波”这一成就而获得了诺贝尔物理学奖。1936年,普雷斯维克(Peter Preiswerk)等人各自独立地发现中子衍射现象,验证了中子的波动性。1999年,维也纳大学(University of Vienna)的研究人员将一束60个碳原子富勒烯分子束通过光栅得到干涉图样,验证了分子的波动性。
物质的波动特性
自从物理学者演示出光子与电子具有波动性质之后,对于中子、质子也完成了很多类似实验。在这些实验里,比较著名的是于1929年斯特曼、斯特恩团队完成的氮原子和氢分子束衍射实验,这实验有效地演示出原子和分子的波动性质。21世纪左右,关于原子、分子的类似实验显示,更大尺寸、更复杂的粒子也具有波动性质。
微观粒子的波动性的可观察性与粒子的德布罗意波长及直径的相对大小有关,粒子的德布罗意波长大于直径则波动性显著,可观察性相对较强,粒子的德布罗意波长远小于直径,则波动性即不显著,可观察性相对较弱,宏观物体的德布罗意波长远小于它的线性尺度,波动性几乎无法观测。
1970年,西拉斐特(West Lafayette)等物理学者使用中子干涉仪完成了一系列实验强调了引力与波粒二象性彼此之间的关系。2003年,维也纳(Vienna)的研究团队验证了四苯基卟啉的波动性。2006年,伊夫·库德(Yves Couder)发布论文表示,宏观油滴弹跳于振动表面可以用来模拟波粒二象性。
研究进展
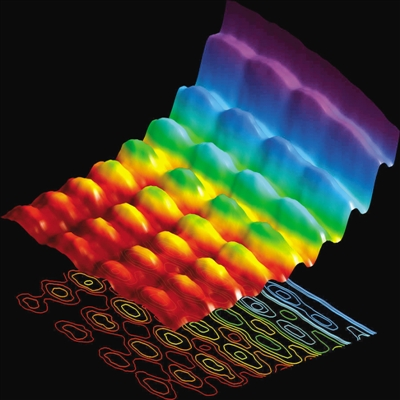
2015年,瑞士洛桑联邦理工学院的科学家成功通过在石墨烯膜上悬浮的单个纳米线上的时空重叠电子和光脉冲拍摄出有史以来第一张光同时表现出波粒二象性的照片。
2021年,中国北京大学的极端光学研究团队在大规模集成光量子芯片上多路径波粒二象性研究中取得进展,通过大规模硅集成多路径干涉仪实现了在惠勒延迟选择条件下粒子的多路径波粒二象性的观测。
应用举例
电子显微镜
电子显微镜借助透过试样透电子束的波动性(透射或衍射)所形成的图像来分析试样内部的显微结构。电子显微镜突破了传统光学显微镜的最大放大倍率,可以观测到更细微的结构,理论上,电子显微镜可比光学显微镜分辨率高10万倍,但因电子显微镜视差及样品制备的问题,分辨率在1nm左右最好。

残余应力检测——中子衍射法
中子衍射法借助中子的波动性(衍射),测量材料的晶格间距从而确定材料在各方向上的弹性应变,应变测量完后,根据广义胡克定律计算得到材料的残余应力值。中子衍射法在测量具有较大体积固体材料的内部残余应力上具有优势,且受到表面效应的影响小,缺点是中子源的流强一般较弱,需要的测量时间比较长,且中子源建造和运行费用昂贵。
光电器件
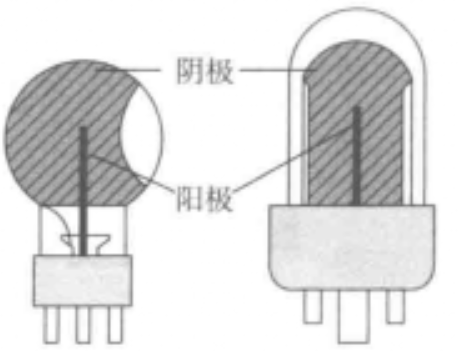
光电器件借助光电效应(光的粒子性),物体(主要是金属)受到射线照射时,有电子从表面逸出,实现光能到电能的转换,进而实现相应的功能,如:光敏二极管、光敏三极管根据光线的照射强弱输出对应强度的电信号,半导体材料P-N结受到光照后产生一定方向的电动势,真空光电管或光电管受到光照后在外电路中产生电流等。
偏光眼镜
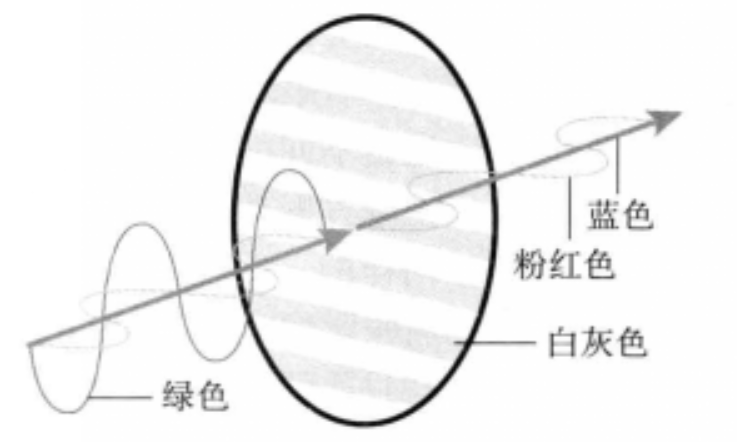
偏光眼镜根据光的波动性,只允许在某个特定方向振动的光可以通过,并且能够阻挡其他方向振动的光通过,进行选择性遮挡以使眼睛看到不同的画面,借助偏光眼镜可实现媒体的3D效果。偏光眼镜的3D效果较好,生产成本也比较低廉,但在使用过程中大幅转动会影响成像效果。
光谱分析
光谱分析测量物质由发生了量子化的能级之间的跃迁而产生的反射、吸收或散射辐射的波长(光的波动性),形成的物质的辐射光谱,不同物质的辐射光谱不同,据此可分析被测物质的化学组成和相对含量。光谱分析灵敏而迅速,包括分光光度法、荧光光谱法、红外光谱法、原子发射光谱法、原子吸收光谱法、原子荧光光谱法等。

研究意义/影响
波粒二象性是一切微观粒子的普遍属性,微观粒子波粒二象性的发现和研究,对量子力学的建立和发展起了重要作用,在微观粒子波动性的基础上建立了波动力学,而随着量子场论的发展,场遵循的波动方程的解被称为波函数。量子场论将粒子视为更基础的场上的激发态,即所谓的量子,而粒子之间的交互作用则是以相应的场之间的交互项来描述。每个交互作用都可以用费曼图来表示,一些以前难以理解的现象得到解释。波粒二象性涉及到对微观客体实在性的认识,及主客体关系与作用等问题。对物理哲学的发展有促进作用。
类似现象理论
粒子波双观
德布罗意曾提出导波理论,认为微观粒子的波函数不是概率波,而是物理空间真实的场,粒子永远有确定的位置和动量,波和粒子同时存在,并在假定中描述了一种粒子和场之间的耦合(粒子骑在波上,波引导粒子而行),将耦合波称为导波,据此解释干涉、衍射现象。
唯波观
源自休·埃弗雷特(Hugh·Everett)的多世界解释认为,微观粒子可由一个宇宙波函数来完全描述,它是多个分支波函数的叠加,整个宇宙状态由一个极其复杂的波函数决定,宇宙波函数从不塌缩,永远按薛定谔方程进行决定性的演化,量子测量过程的相互作用导致了宇宙波函数的演化。
量子叠加
量子叠加是指一个量子系统的能量、自旋、运动场等量子态的所有可能状态同时存在,这种所有可能状态同时存在的状态叫做量子叠加态。