角动量守恒定律是物理学中重要的基本原则之一。它指出，在一个孤立系统中，当没有外部扭矩作用时，系统的总角动量将保持恒定。质点的角动量定理为

\frac{dL}{dt}=r\times F
，其中
\frac{dL}{dt}
是质点对固定点的角动量对时间的微商，
r\times F
是作用于该质点上的力对该点的力矩。角动量是一个广泛的量，任何复合系统的总角动量是其组成部分角动量的总和。

开普勒第二定律是角动量守恒定律的最早表述。十七世纪初，约翰尼斯·开普勒（Johannes Kepler）通过对火星绕太阳的运动进行观测，发现火星运行时的面速度是不变的，这就是”面积定律“。随后，艾萨克·牛顿（Isaac Newton）从理论上推导出了角动量守恒定律。

角动量有方向和大小，而且都是守恒的。特定相互作用的角动量变化称为角冲量，也称旋转。与线性动量守恒类似，如果没有外力矩，角动量守恒。不同的是，角动量取决于选择原点的位置，因为粒子的位置是从原点测量的。因此在研究物体转动问题时，角动量可以作为动量的补充来描述机械运动。

角动量守恒定律在经典力学、量子力学以及天体物理学中都有广泛的应用。自行车、飞盘、膛线子弹和陀螺仪的有用性质都可以用角动量守恒来解释。角动量守恒也是飓风形成螺旋和中子星具有高旋转速率的原因。

本页面主要目录有关于角动量守恒定律的：发展历史、定义、原理、应用等介绍

中文名

角动量守恒定律

外文名

law of conservation of angular momentum

表达式

L = mvr

应用学科

物理

提出者

艾萨克·牛顿（Isaac Newton）

发展历史

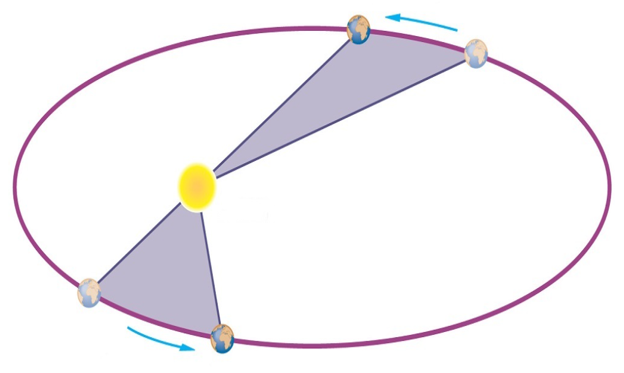
自从开普勒提出了他的第二行星运动定律，人们就已获知，在相同的时间间隔内，太阳和行星之间的连线扫过的面积是相等的。牛顿提出了独特的几何证明，进一步证实了太阳引力的吸引力是导致所有开普勒定律的原因。在《原理》一书中，牛顿在讨论第一运动定律的例子时，暗示了角动量的概念。他通过对面积定律的几何证明，间接证明了在受到中心力的情况下，角动量是守恒的。

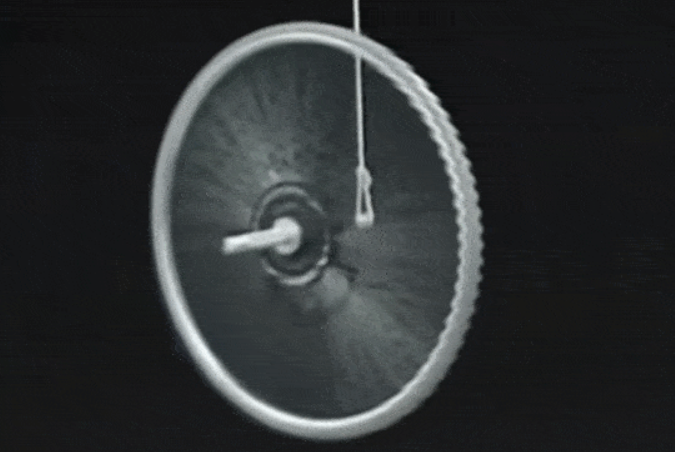
莱昂哈德·欧拉（Leonhard Euler）、丹尼尔·伯努利（Daniel Bernoulli）和帕特里克·达西都（Patrick Darcy）都从面速度守恒的角度理解角动量，这是他们对开普勒行星运动第二定律分析的结果。1736 年，欧拉像牛顿一样，在《力学》一书中提到了一些角动量方程，但并未对这些方程进行进一步的探讨。 伯努利在1744 年的一封信中写到了“旋转运动的力矩”，这可能是我们现在理解的第一个角动量概念。1799 年，皮埃尔-西蒙·拉普拉斯 (Pierre-Simon Laplace)首次意识到固定平面与旋转相关——拉普拉斯不变平面。路易·波因索（Louis Poinsot）于1803年开始将旋转表示为垂直于旋转的线段，并详细阐述了“力矩守恒”。1852 年，莱昂·福柯（Leon Foucault）在一项实验中使用陀螺仪来显示地球的自转。

威廉·兰金（William Rankine）在1858 年的《应用力学手册》首次定义了现代意义上的角动量：一条线，其长度与角动量的大小成正比，其方向垂直于物体和固定点的运动平面。当从线的末端观察物体的运动时，物体的半径矢量符合右螺旋法则。

定义

经典力学中的定义

二维轨道角动量

角动量是一个矢量（更准确地说，是伪矢量），表示物体绕特定轴的旋转惯量和旋转速度（以弧度/秒为单位）的乘积。然而，如果粒子的轨迹位于单个平面内，则可以忽略角动量的矢量性质，并将其视为标量（更准确地说，伪标量）。角动量可以被认为是线性动量在旋转过程中的表现。因此，正如线性动量

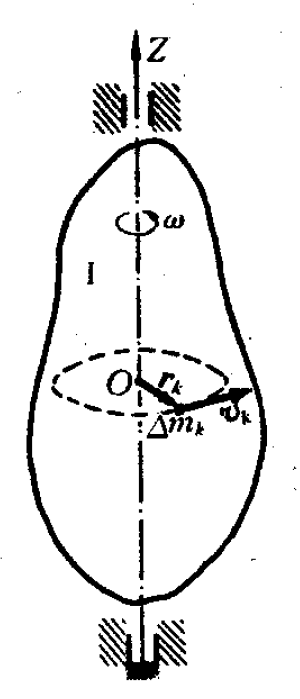
角动量守恒定律

将两边投影到质点k圆轨迹切线方向，有：

角动量守恒定律

工业技术

角动量守恒定律在实际应用中有很多优势。在蒸汽机或内燃机等发动机中，常常需要使用飞轮，这个装置能够有效地将活塞的横向运动转化为旋转运动。惯性导航系统就是利用了角动量相对于空间惯性系守恒的原理，使得潜艇能够在极地冰盖下航行，同时对于所有现代导航方式都至关重要。旋转的陀螺具有很好的定轴性，这也是因为其遵守了角动量守恒的原理，即在没有外力矩的作用下，物体的角动量会保持恒定。在工业中，可以看到很多这样的例子，比如子弹从枪膛里出来时高速旋转，这样就能够保持稳定性和准确性。角动量守恒定律还可以用来实现卫星的定向控制。而在一些轿车上，就安装了测量车身纵向和横向摆动的陀螺传感器，这样可以实现车身稳定度的控制。

在骑车的时候会发现骑得越快，越容易保持平衡，是因为在陀螺效应的作用下，轮子克服了重力，形成了进动，通过改变方向维持了自身平衡。而这种平衡状态与车轮的速度有关，速度越快，车轮的倾角越小，车身越稳定

角动量守恒定律