中考数学经典试题,如何解决几何图形中的折叠问题?
中考数学经典试题,如何解决几何图形中的折叠问题?
-
很高兴能回答这个问题,作为一名初中数学老师,我来讲讲关于这个问题的看法。
在初中阶段,折叠问题是个经常出现的问题,通常叫作翻折。这类题型既是中考常考的题型,在各年级的期中期末考试中也经常出现。经常以填空题和压轴题的形式出现,填空题比较容易,压轴题稍微复杂一点。只要熟练掌握了这类题的解题方法,其实非常简单。
解决翻折问题,要把握三个原则:
(1) 有翻折必有重合,重合即意味着相等,重合的角和边都是相等的;
(2) 如果翻折中出现直角三角形,通常会用到勾股定理;
(3) 如果勾股定理得不出结果,可以考虑运用相似三角形进行求解。
根据这三个解题原则,结合常见的题型,下面来仔细讲一讲。
类型一:运用勾股定理求边长
例1、如图所示,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为_______
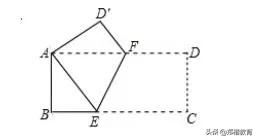
解题策略:解决该题分为三步:
第一步,找出相等的边和角,根据重合即相等的原则,可以从图中明显看出,AE=EC,<AEF=<CEF,再结合AD//BC,可以得出三角形AEF为等腰三角形,即AE=AF;
第二步,设BE=x,则AE=EC=16-x,然后在直角三角形ABE中,利用勾股定理列方程即可得出x=6,进而得出BE=6,AE=AF=10;
第三步,过点E向AF作垂线,可以得出高线与AB相等为8,再运用勾股定理即可求出EF为2倍根号5.
类型二:运用相似求边长
例2、如图,已知在Rt△ABC中,∠B=90°,AB=1,BC=2,点E、F分别在边AB、AC上,联结EF,将△AEF沿着EF翻折,使得点A落在边BC上的点D处,且FD⊥BC,那么ED=( ).
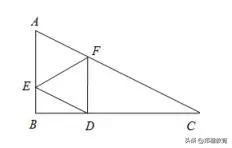
解题策略:
第一步:利用重合即相等的原则,可以轻易得出三角形AEF与三角形DEF相似,即AE=DE,AF=DF,<A=<EDF;
第二步,结合已知条件FD⊥BC,三角形EBD与三角形ABC相似,又由AB=1,BC=2可知,BD与BE也是两倍关系,如果设EB为x,则BD为2x,AE=DE=1-x;
第三步:在直角三角形EBD中,运用勾股定理列出关于x的方程,可以轻易求出ED。
下面是一些类似的题目,可以利用上述方法试一试。
巩固练习:
1、如图所示,在一张矩形纸片ABCD中,AD=4cm,点E、F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_______
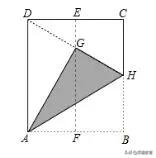
2、如图,矩形纸片ABCD沿EF、GH同时折叠,B、C两点恰好同时落在AD边的P点处,若∠FPH=,PF=8,PH=6,则图中阴影部分的面积为__________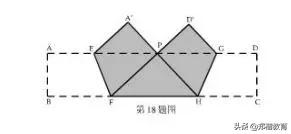
3、如图所示,在Rt中,,,BC=1,点D在边AC上,将沿直线BD翻折后,将点A落在点E处,如果,则线段DE的长为________________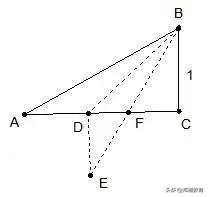 2019-08-14 23:04:25
2019-08-14 23:04:25 -
折叠问题,最关键的一条就是要弄清楚折叠前后哪些变和不变。其次要熟悉相应的性质,对基础知识和基本概念要清楚。
2019-08-14 16:34:56 -
折叠就意味着有相等的线段和角等图形。你要根据折叠首先找到这些,然后看看哪些是有用的信息,能否转化到一个三角形中利用勾股定理解方程?
2019-08-14 19:06:54
