为什么做功可以和力向量与位移向量的特定内积得出？

首先我们要知道，做功其实就是能量变化的量度，做了多少功，说得就是能量变化了多少。题主说的力向量与位移向量的特定内积得出的功其实表征提动能的变化量，其他能量的变化并不能由力向量与位移向量来表示，比如电功。

在题主的问题中，我们只关心做功与动能的变化量，其实就是动能定理：合外力对物体所做的功，等于物体动能的变化量。力与位移在同一直线的运动的动能定理推导如下：

由此，我们可以得到动能的变化量其实就等于力与位移的乘积。那为什么后来更一般的式子是动能的变化量等于力向量与位移向量的内积呢？

这是因为力的方向不一定与位移的方向一致。如下图，当力与位移方向不一致时，力F可以分解成平行和垂直位移L的两个力F1和F2，因为F2不做功，所以F做的功等于F1·L（力F1乘以位移），而F1·L的值等F·Lcosθ（即力F与位移L的内积），所以物理学中为了更一般化，都是用力向量与位移向量的内积计算机械功，也就是动能的变化量。

最后更正一下题主的问题，做功其实就是能量的变化量，力向量与位移向量的内积只能算动能的变化量，算不了其他能量的变化量，也就是说力向量与位移向量的内积只能表示机械功。

物理学作为一门研究物质运动最一般规律和物质基本结构的学科，观察、实验和推理是其研究的重要手段。

通过观察大量经验事实时发现:由于施力物(人或其它生物、非生物)在至少与施力方向不垂直的方向上发生位移时，客观上伴随着能量变化(转移或转化)(见下面的示意图)，即:当该作用力F在与位移S的方向在同一直线上的方向上的分力F1与位移S的方向相同时，该力F做正功，施力物的能量被消耗，当该分力F1与位移S方向相反时，该力F做负功，施力物的能量得到补偿，且消耗或补偿的这部分能量W的大小与该分力F1的大小Fcosθ和该位移的大小S都成正比，当然，该施力物在与施力方向垂直的方向上发生位移时，客观上并没有做功，没有发生能量变化。由此总结出自然界的一大普遍运动规律——当力F对物体做功时，其变化的这部分能量的大小，即做的功的大小W = FcosθxS = F1xS = FS = FScosθ = FⅹS1 = FxS1 = |F||S|cosθ。从该公式可以看出，做功大小W可由F与S的内积(也叫点积、数量积、标量积、向量的积)计算出来，该力做的功的大小W还与该力F的大小F和在该力作用下发生的这段位移S在与该力F的方向在同一直线上的方向上的分位移S1的大小S1都成正比。其中，所有加粗的字母表示向量或矢量，|F|和|S|表示F和S的大小，是与这两种矢量对应的标量，θ为该力F方向与位移S方向的夹角，θ∈[0，π]。

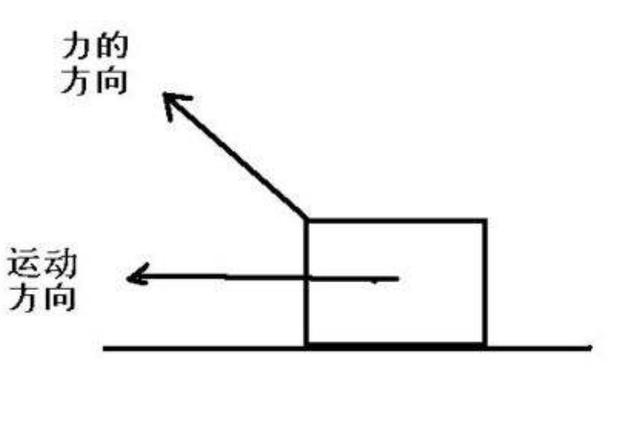
外力F对物体做功示意图

(声明：文中图片来自网络，版权归原作者及原出处所有。如涉侵权或原版权所有者不同意转载，请及时联系我，以便立即删除。但内容系个人原创，可读性强，欢迎广大读者朋友品阅，不吝赐教。如需转载，请注明出处！)