为什么反比例函数图像跟坐标轴无限接近？

当一根绳子正沿着另一曲线（假设曲线是圆）绕上或脱下时，它描出一条渐伸线。

渐伸线的形状就像上图中点 B 的运动轨迹 。

当曲线 C 上动点 P 沿着曲线 C 无限远移时，若动点 P 到某直线 L 的距离无限趋近于 0 ，则称直线 L 是曲线 C 的渐近线 。

曲线的渐近线有两种类型：

1、垂直渐近线；

2、斜渐近线（包括水平渐近线）。

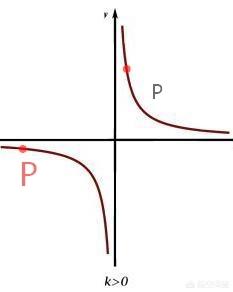
在反比例函数 y = k/ x （k>0）的图像中，

在第一象限中 ：

①当动点 P 沿着 x 轴无限远移时，即 x 趋于 ∞（无穷大时），y = k/ x 的极限值是 0 （无穷小），此时动点 P 到 X 轴的距离趋于 0 ，我们把 x 轴称为反比例函数图像的 水平渐近线 。

②当动点 P 沿着 x 轴无限接近 y 轴时，即 x 趋于 0 （无穷小）， y = k/ x 的极限值是 ∞ （无穷大），此时动点 P 到 y 轴的距离趋于 0 ，我们把 y 轴称为反比例函数图像的 垂直渐近线 。

其它象限同理。

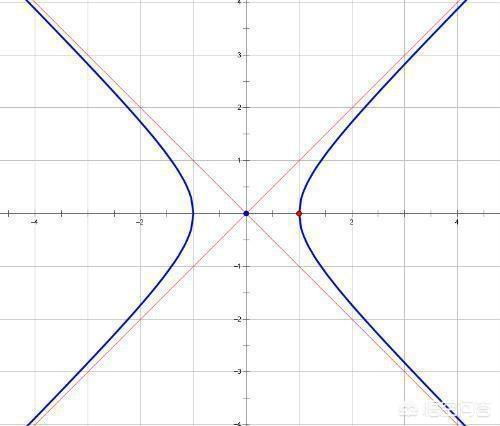
如上图中 y = ±x 是 双曲线 C 的斜渐近线 。

在反比例函数 y = k/x ( k ≠ 0 )的图像中：

当 x 趋于无穷小时， y 趋于无穷大；当 x 趋于无穷大时，y 趋于无穷小 ，此时的图像才跟坐标轴无限接近。

注：无穷大包括正、负无穷大。

从算式的角度可以这样理解：随着X无限增加，其反比例函数必然无限缩小，表现出来就是无限接近于横轴。

你这个问题的关键在于"无限"二字，所谓无限接近就是当X值大到很大很大的时候，其实就是反比例值和0相等的意思。如何理解无限接近的感觉，可能学过极限理论比较好理解。

举个现实生活中的例子来说明极限：你吃甘蔗，每次吃剩下长度的一半。假设你的生命不止，那么这根甘蔗是不是吃不完？哈哈。事实是，甘蔗很快就会吃完。

这个反比例函数跟坐标轴可以无限接近，你如果熟悉极限的概念就不会由次疑问了。使用δ-ε语言可以表述清楚，对于任意的ε>0，都有x>δ=[1/ε]+1，使得|1/x - 0|<ε。就是说反比例函数可以无限的接近坐标轴但是不相交。

证明不相交，用反证法，设存在1/x=0的解，x0，那么有x0=1/0，这个数不是确定值。

一个初中生提出这个问题，就要从初中生能理解的程度来解答：

1.为什么不与坐标轴相交?

反比例函数关系式y=k/x(k不等于0),自变量x位于分母上，因为分母为0，分式无意义，所以x不会等于0，y也不会等于0.

而x轴上的点横坐标等于0，y轴上点纵坐标为0.双曲线如果与x轴有交点，就与x不等于0矛盾，所以双曲线与x轴永远不会相交。如果双曲线与y轴有交点，就于y值不等于0矛盾,所以双曲线与y轴永远不会相交。

2.为什么与坐标轴无限接近?

因为k为不等于0的定值，当k大于0时，比如x=2，随着x绝对值的无限増大，2/x的绝对值就无限减小，即双曲线上的点的纵坐标绝对值无限小，所以双曲线越来越接近x轴，随着x绝对值的无限减小，2/x的绝对值就无限增大，即双曲线上的点的纵坐标的绝对值越来越大，所以双曲线越来越接近y轴。当k小于0时，道理相同。

问出这个问题的朋友很可能是初中生，所以如果要回答，当然要用最基础的语言来回答。从问题描述来看，你对反比例函数本身的理解完全没有问题，你也已经看到，的确随着x的增大，函数值在越来越靠近0，所以曲线随着自变量x的增大不断靠近x轴。

然而，在提问的语言中，你犯了一个逻辑错误。这个错误就在于，认为「渐渐接近」就是有「交点」。这是完全错误的，因为「交点」跟「渐渐接近」本身就是矛盾的，有了「交点」，就没有继续「渐渐接近」了。因为有了交点之后，只可能出现两种情况。一种是从交点处开始「渐渐远离」，例如各种曲线的切线就都是这样的情况。另一种情况是，从交点处开始，两条线完全重合，产生出有无限多个交点，这就不叫「渐渐接近」了，而是两条线从某处开始一直贴在一起没有变化过。也就是说，不管是哪种情况，只要有交点，都违背了最初我们想要的「渐渐接近」。因此，「渐渐接近」就是没有交点，如果一定说要有，那也是在无穷远处。在以后的课程学习中，你还会遇到很多很多的「渐近线」，不但双曲线有，三角函数（例如正切函数）和反三角函数，各种分式函数，Logistic函数……都有渐近线，所有的「渐近线」都跟函数本身是没有交点的。

一个初中生，对这样基本的问题产生疑问是一件很好的事情，相关的内容在高中数学选修课上学过极限的概念之后就可以明确了。